2021. 1. 2. 10:07ㆍ언어영역/Machine Learning
원핫인코딩
범주를 회귀와 같은 방식으로 계산한다면 다양한 품종의 꽃들이 "품종"이라는 한 개의 속성으로 분류될 것이다. 하지만 우리가 원하는 건 품종 중에서도 어떤 품종인지, 즉 "Setosa", "Versicolor", "Virginica"(아이리스 꽃 품종의 종류)인지를 구분하는 것이다. 이를 위해서는 '품종'속성을 새로운 칼럼들(=속성)로 바꿔준다. 이 과정을 원핫인코딩이라고 하며, 아래 예시를 통해 이해하자.
기존 표
| 꽃잎의 길이 | 꽃잎의 폭 | 품종 |
| 5.1 | 3.5 | Setosa |
| 4.9 | 3 | Virginica |
적용 코드
아이리스 = pd.get_dummies(아이리스)
변환된 표
| 꽃잎의 길이 | 꽃잎의 폭 | 품종.Setosa | 품종.Versicolor | 품종.Virginica |
| 5.1 | 3.5 | 1 | 0 | 0 |
| 4.9 | 3 | 0 | 0 | 1 |
이렇게 판다스 코드 한 줄을 통해 범주형 데이터를 컴퓨터가 읽기 쉽도록 변환시킬 수 있다.
활성화함수
영상에서 Sigmoid와 Softmax의 차이점을 숙제로 내 줬다. 아무래도 영상 안에 담기엔 중요성이 떨어지고 개념이 어렵기 때문이겠지. 다음은 그 과제물이다.
활성화 함수에 대해 검색해봤다.
In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs.
-Wikipedia
번역하면 "인공신경망 학문에서, 노드에서의 활성화함수는 입력된 정보(또는 그 데이터세트)를 고려해 그 노드의 출력물을 정의한다." 정도가 되겠다. 다시 말해서, 입력값을 우리가 사용하기 편하도록 함수에 넣어서 편하게 바꾼다는 거다.
예를 들어, 우리가 배운 퍼셉트론(또는 Neural Network의 약자를 써서 NN이라고도 하나보다. 헷갈리네...)은 y=wx+...+b가 되는데, 이 때 활성화함수는 h(x)=x 그 자체이다. 회귀 모형에서는 굳이 데이터 모양을 바꿀 필요 없이 그대로 출력되기 때문이다. 하지만 분류 모델에서는 그대로 수치를 쓸 수 없다. 분류할 수 있도록 바꿔줘야 한다. 실제로 사용되는 활성함수에는 여러 종류가 있고 주로 비선형함수를 사용하는데, 이는 선형함수가 특성상 합성함수를 이용해도 그 깊이가 깊어지지 않기 때문이다(일차함수 백번이고 합성해봐라 일차함수지). 활성함수에는 일단 몇 가지 종류가 있다.
-
Step Function
-
고등학교 때 자주 봤던 절댓값이 붙어있는 함수라고 생각하면 된다. 독립변수를 함수에 넣은 결괏값이 특정 수치를 넘어가면 1, 아니면 0과 같은 식으로 분류하는 함수이다.
-
-
Sigmoid Function(-->Softmax Function)
-
위 Step Function은 0과 1로만 표현이 된다. 이보다 더 많은 정보를 담기 위해서 고안된 게 바로 Sigmoid function인데, 이는 완만한 S자 모양을 하고 있어서, 독립변수를 함수에 넣은 결괏값 수치가 커질수록 1에 가까워지고, 작을수록 0에 가까워진다.
-
-
ReLU function
-
최근에 많이 쓰인다고 한다. 독립변수를 함수에 넣은 결괏값 수치가 특정 수치 이전에는 0을 유지하다가, 특정치 이상으로 올라가면 1차함수의 모양으로 점점 증가하는 형태를 띈다.
-
- 등등

Sigmoid함수와 Softmax 함수의 차이점을 알기 위해서는 아직 알아야 하는 게 몇 개 더 있다. 그것부터 먼저 살펴보도록 하자.
Cross Entropy
먼저 우린 Cross Entropy에 대해서 알아야 하는데, 이걸 알려면 그 전에 먼저 Entropy, Logits 등에 대해서 알아야 한다. 뭐 이렇게 알아야 할 게 많냐고? 그러게말이다. 쓰는 나는 오죽했겠니...
Entropy
엔트로피를 알기 위해서는 아래 영상이 도움이 많이 된다. 읽는 것보다 이게 나을거다.
엔트로피란 무엇인가 : youtu.be/r3iRRQ2ViQM
섀넌 엔트로피 자세한 설명 : youtu.be/CdH7U3IjRI8
내 필기를 위해 다시 설명하자면
첫째, 엔트로피는 불확실성을 의미한다.
어느 확률이 어느 한쪽으로 치우쳐져있지 않고 분산돼있을 때, 우리는 도대체 어떤 사건이 일어날지에 대해서 알 수가 없다. 그리고 도대체 얼마나 알 수 없는가를 표현하는 게 엔트로피이다. 그리고 이건 '정보량'이라는 개념에도 대입 가능한데, 앞으로 잘 살게 눈에 뻔히 보이는 내 옆에 잘나가는 친구보다는 한치앞을 알 수 없는 블록버스터같은 내 인생이 더 많은 정보를 지니고 있지 않을까? 그러니 엔트로피가 낮을수록(확실할수록), 정보량은 낮아지고, 엔트로피가 높을수록(불확실할수록) 정보량은 증가한다. 엔트로피 높은 내인생
그렇다면 엔트로피를 구하는 방법은 몰까? 먼저 식부터 보자.

상당히 복잡해보이지만 사실 맹탕이다. Log부분을 그냥 변수 x라고 생각하면 기댓값을 구하는거나 다름없기 때문이다. 로그 부분이 사건의 '정보량들' 이라고 쳐 보자. 그렇다면 위 식은 정보량의 기대치이다. 동전을 한번 던져보면 무슨 소린지가 쉽게 이해된다. 우리가 동전을 던졌을 때 이 사건의 엔트로피(=동전 던지기라는 사건의 정보 기댓값) = (앞면이 나오는 사건에 대한 정보량)*(앞면이 나올 확률) + (뒷면이 나오는 사건에 대한 정보량) * (뒷면이 나올 확률)인거다. 오! 그럼 이제 나는 동전을 한 번 던졌을때 대충 얼마의 정보량이 나올지 예측할 수 있다.
관건은 이제 그 '로그 부분', 다시 말해서 '정보량들'이다. 앞면이 나올 확률의 정보량이면 그냥 정보량인거지 왜 저렇게 복잡하게 해 놨을까? 이유는 두 가지다. 첫째, 확률이 높으면 정보량이 낮고, 확률이 낮으면 정보량이 높다. 둘째, 두 사건의 정보량의 합은 두 사건이 다 일어났을 때의 정보량과 같다.
먼저 첫째이다. 확률이 높으면 정보량이 낮고, 확률이 낮으면 정보량이 낮다. 어떡하지? 간단하다. 확률에 역수만 취해주면 된다.
이제 로그만 남았다. 두 사건의 정보량의 합은 두 사건이 다 일어났을 때의 정보량과 같다. (A와 B가 일어날 사건의 정보량) = (A사건의 정보량) + (B사건의 정보량)과 같은 형태가 돼야 한다는 거다. 이해하기 쉽도록 I(x)가 정보량 함수라고 생각해보자. 위에서 말로 풀어놓은 건 I(A와 B가 동시에(둘 다) 일어날 확률)=I(A가 일어날 확률)+I(B가 일어날 확률) 이렇게 될 거다. 자세히 봐봐. 아니 다시 한번 봐. A와 B는 독립사건이니 f(A*B)=f(A)+f(B)다. 이런 함수가 뭐가 있을까? 바로 Log다. Log(AB)=Log(A)+Log(B)니까. 그래서 로그를 붙여주는 것이다.
로그 아래에 2를 붙일 수도 있고 e를 붙일수도 있다. 컴퓨터에서는 2를 붙인다(섀넌 엔트로피). 이렇게 하면 출력된 엔트로피를 바탕으로 몇 비트(bit)가 필요한지에 대해서 알 수 있기 때문이란다. 확률에 대해서는 e를 붙인다(나츠 엔트로피). Softmax 과정에서 정규화를 위해 지수의 제곱으로 들어가기 때문이다.
Cross Entropy
그렇다면 크로스 엔트로피는 무엇인가? 일단 크로스 엔트로피가 어디에 속하는지에 대해 알아야 한다. 바로 손실함수이다. 그래. 회귀모델에서 손실함수는 MSE였잖아. 그런 것처럼 분류 모델에서는 CE를 쓴다는 의미다. 다시 말해서, CE는 '모델에서의 정보량이 실제 정보량과 얼마나 비슷한가?'를 측정해주는 방식이다. CE는 실젯값과 비슷하면 비슷할수록 0에 가깝게 나온다.

크로스엔트로피를 구하는 방법은 위 그냥 Entropy를 구하는 방법과 거의 흡사한데, 그 '로그 부분'에 p가 아니라 우리가 만든 모델의 확률을 대신 집어넣어주면 끝이다.
그 이유는 바로 '로그 부분'이 사건의 정보량을 의미하고, 우리는 우리가 구한 모델의 정보량(엔트로피)이 실제와 유사한지에 대해 판단해야하기 때문이다. 그리고 실제로 그 사건이 일어날 확률은 실제 사건을 기반으로 하는게 정상이고. 참고로 사진을 자세히 들여다보자. 실제의 상황에서는 위 스크린샷처럼 세 개중 하나의 사건만 발생한다. 그러므로 실제 확률은 (1,0,0)과 같은 형태가 된다. 이제 다 끝나간다! 올레!
하지만 한 가지 중대한 문제가 남았다. 바로 우리가 갖고있는 데이터가 위 사진처럼 확률로 표현되지 않았다는 것. 우리가 갖고있는 데이터는 마이너스 무한대부터 무한대까지 이를 정도로 넓은 스펙타클한 범위를 자랑한다. 이를 확률의 형태로 바꿔서 Cross Entropy 손실함수에 우겨넣을 수 있도록 바꿔줘야 한다. 이 때 등장하는 게 바로 우리의 영원한 친구, 활성화함수 Sigmoid와 Softmax이다. 여기를 많이 참조했다. (그냥 거의 다.)
하지만 우리가 그 전에 알아야 할 것이 하나 남았으니 Logit이다. ㅎㅎ...
Logit
Logit은 Log Odds의 약자란다. 아니 로고즈 줄여서 로짓이 된건가..? 차라리 Logos가 더 말이 되겠다. 뜻도 좋구만. 여튼, Log Odds는 Odds에 로그를 씌운 걸 의미하는데 Odds는 사건 발생 확률의 비율이다. 그러니까 예를 들어서 A, B로만 이루어진 사건이 있다면 A/B는 A의 Odds이고, B/A는 B의 Odds가 되는 것이다. 그럼 이런 Odds는 왜 구하는 걸까? 분류를 위해서이다. Odds에 로그를 씌운 Logit 값이 양수라면 A로 분류하고, Logit 값이 음수라면 B로 분류하는 식이다. (굳이 양수 음수일 필요는 없다. 순서 바뀌어도 된다.)
Sigmoid
그냥 Odds만 써도 될거에 굳이 Log를 붙여서 되도않는 Logit을 만든 이유는 뭘까? 바로 Sigmoid Function을 만들기 위해서이다.
우리가 NN에서 얻은 값을 z라고 한다면, 이건 확률이 아니라 그냥 수치다. 이 수치를 0과 1사이의 확률로 바꾸기 위해서는 Logit을 이용하면 된다.

우리가 구한 식이 Logit와 같다고 두고 방정식을 세워보자. y는 특정 사건이 일어날 확률을 의미한다. 로그를 없애기 위해 자연상수를 사용했다.
이렇게 된 식을 y에 대해 정리하면 다음과 같다.

이러면 실수 z에 대해서 y는 0과 1 사이의 값으로 표현할수 있게 된다. 즉, 우리가 갖고 있던 z로, 구하고 싶었던 0과 1 사이의 수치 즉 확률을 도출해낸 것이다. 하지만 문제가 있다. 이 수치는 딱 확률이 두 가지로 양분되는 경우에만 쓸 수 있다는 것이다. 다시 말해서, 동전 던지기에만 쓸 수 있는 모식이다.(...)
Softmax
이를 해결하고자 혜성처럼 등장한 것이 바로 Softmax이다. 클래스, 즉 속성의 개수가 3이상일 때를 위해서 Odds를 다르게 두고 계산을 함으로써 정의한다는 건데 솔직히 나는 Odds의 설정 부분이 잘 이해가 가진 않는다. 그냥 그러려니 할 뿐 (...) 여기를 참고했다. 식 이해하는 분은 알려주셨으면 좋겠다. 왜 두 번째 식의 분모가

이렇게 나오지 않는지... 아무래도 내가 바본가...?
어쨌든 이러한 계산을 완료하고 나면
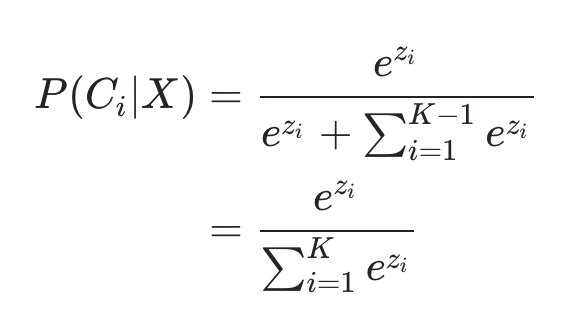
이런 식이 등장하게 된다. 식을 다시 한번 풀이하게 되면 exp(특정 사건의 Odd)/sig(exp(사건들 각각의 Odd)) 이라는 형태가 된다. 즉 다른 변수들까지 고려해서 확률값이 0~1사이에 있을 뿐만 아니라, 3개 이상의 변수에서도 확률값 총합이 1이 되도록 변형된 것이다.

다 하고 나서는 그냥 처음부터 확률을 구하면 얼마나 좋았을까 하는 생각이 든다. 하지만 어쩔까, 우리가 얻은 수치는 아쉽게도 확률이 아니고, 없는 데이터에서 손실 함수를 이용해 모델이 얼마나 맞는지 맞추는 건 우리의 몫인 걸. 다행인 점은 이 모든 복잡한 과정은 우리는 생각할 필요도 없이 코드 두 줄이 다 해결해준다는 것이다. 하도 영상을 찾아보다보니 새벽에는 심지어 이분에 대한 위인전까지 추천 영상에 떴다. 이런 천재적인 사람의 명석한 생각을 통해 나같이 식도 이해 못하는 바보가 원리도 모른 채 크로스 엔트로피라는 손실함수를 사용하고, 이를 위해 활성함수를 통해 데이터를 멋대로 조작할 수 있다는 사실이 너무나도 놀랍다. 언젠가 나도 이런 생각을 해낼 수 있을 때까지, 아니면 이런 생각을 마치 자기 것인 양 활용할 수 있을 때까지 공부해야겠다. 그리고,
영상에서 하는 말은 듣자. 괜히 영상에서 중간에 보지 말고 공부가 다 끝나고 보라고 한 게 아니라는 걸 뼈저리게 느낄 수 있었다.
REFERENCE
슈퍼짱짱 블로그
Gaussian37
딥 러닝을 이용한 자연어 처리 입문
youtu.be/r3iRRQ2ViQM
youtu.be/CdH7U3IjRI8
velog.io/@gwkoo/logit-sigmoid-softmax%EC%9D%98-%EA%B4%80%EA%B3%84
'언어영역 > Machine Learning' 카테고리의 다른 글
| Tensorflow 102 5-6 특징 자동 추출기 (0) | 2021.01.13 |
|---|---|
| Mahcine Learning 야학 102 - 1~4, 차원 알아보기 (0) | 2021.01.10 |
| TensorFlow 101-13 회귀모형 인공지능의 원리 (0) | 2020.12.31 |
| TensorFlow 101-1~101-12 (0) | 2020.12.30 |
| TensorFlow 101 공부 시작! (0) | 2020.12.26 |